Answer to 3.a.

Given that,

t (Tax rate on nominal interest rate) = 25%

i (Before-tax Nominal interest rate) = 10%

i^t (After-tax Nominal interest rate) = i(1-t) = 10%(1-0.25) = 7.5%

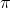(Inflation rate) = 5%

Let r be the before-tax real interest rate and r^t be the after-tax real interest rate.

Formula: i = r +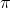 

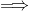 r = i -  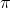....................... (1)

Further, i^t = r^t +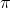 

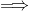 r^{t =} i^t -  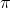........................ (2)

Using equation (1),

Before-tax real interest rate (r) = 10% - 5% = 5%

Using equation (2),

After-tax real interest rate (r^t) = 7.5% - 5% = 2.5%.

Answer to 3.d.

Given that,

r^t remains at 2.5%

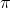 = 6% (5%+1%)

t = 25%

Let i be the before-tax nominal interest rate.

r^t = i (1-t) -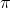 

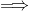 2.5% = i(1-0.25) - 6%

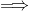 i (0.75) = 2.5% + 6%

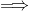 i = 8.5%/0.75

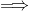 i = 11.33%

Earlier i was at 10% but due to 1% point increase in inflation, keeping r^t constant at 2.5%, i increased to 11.33% i.e. 1.33% increase which is 1.33 multiple times the increase in inflation rate.

Hence as per "Fisher Effect", in case of an economy in which nominal interest rates are taxed, in order to keep the real interest uneffected by the change in inflation rate, the nominal interest rate increases by some multiple of the increase in the inflation rate i.e. there is one-to-one relationship between inflation and nominal interest rate.

If real interest rate is taxed instead of nominal interest rate, then the results would be as follows:

r = i -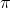 

Keeping i = 10% and 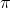 = 5% and t = 25%

r = 10% - 5%

r = 5%

r^t = 5% (1-0.25) = 3.75%

Hence, in order to keep after-tax real interest rate at 3.75%, before-tax nominal interest rate changes as follows to incorporate 1% point increase in inflation as follows ie.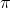 = 6% :

3.75% = (i - 6%)(0.75)

3.75%/(0.75) = i - 6%

i = 5%+6%

i = 11%

If the real interest rate is taxed instead of nominal interest rates, an increase in nominal interest rate before tax by 1% point is required to compensate 1% point increase in inflation so that real interest after tax remains same.