Solution:

Given that,

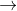 Consider the production function for tomatoes: y = AFaSb, where y is the quantity of tomatoes, F is the quantity of fertilizer and S is the number of sprayings of pesticide during the growing season.

All other inputs are fixed and represented by A > 0. The constants a and b are each positive, but each is less than 1.

i.e,

Production function, y = A*F^a * S^b

(a).

Suppose both quantity of fertilizers and frequency of spraying are increased by proportion, t, then , new output,

y' = A*(tF)^a (tS)^b = t^(a+b) A*F^a * S^b = t^(a+b)*y

If a + b > 1, then the output increases by more than proportion, t, hence, production function exhibits increasing returns to scale.

If a + b < 1, then the output increases by less than proportion, t, hence, production function exhibits decreasing returns to scale.

If a + b = 1, then the output increases by equal to proportion, t, hence, production function exhibits constant returns to scale.

(b).

Marginal product of fertilizer, MPF = dy/dF = a*A*F^(a-1) * S^b

To determine how MPF responds to increase in frequency of spraying,

dMPF/dS = a*b*A F^(a-1) S^(b-1)

As both a and b are positive constants, so, the marginal product of fertilizers increases with increase in frequency of spraying.

(c).

Elasticity of output with respect to spraying = (dy/dS)*S/y = (b*A*F^a S^(b-1))*S/(A*F^a S^b) = b

Thus, elasticity of output with respect to spraying is b.