Why Choose Us?
0% AI Guarantee
Human-written only.
24/7 Support
Anytime, anywhere.
Plagiarism Free
100% Original.
Expert Tutors
Masters & PhDs.
100% Confidential
Your privacy matters.
On-Time Delivery
Never miss a deadline.
Economics Fall 2016 Managerial Economics Take Home This exam covers the material in Chapters 7, 8, 10-11 as well as the accompanying outside readings
Economics
Fall 2016
Managerial Economics
Take Home
This exam covers the material in Chapters 7, 8, 10-11 as well as the accompanying outside readings. This is an economics class. One tenet of economics is that people are rational in their allocation of resources amongst competing ends. Your resources are the readings and time. Since this is a take-home exam, you have access to all necessary information. I will expect you to utilize all the information, since, as rational agents, you know that if you do not, then someone else will, and that person will get the better grade.
One final hint. I am NEVER asking for your opinion. The answer to any “True, False, Explain” questions comes from the course material, not what you already believe or think.
1) Let a production function exist such that Q=K.33L.67
.
Let the firm have a total of $1,000 to spend on labor and capital. Let price of labor equal $5 and the price
of capital equals $10.
a) Write out the total cost (isocost) equation.
b) Find the optimal usage of K and L and the optimal output of Q. (Keep K on the vertical axis and L on the
horizontal).
c) Calculate and plot the isoquant for the optimal Q found in b) given the values for K in the table below. Plot
with the isocost. Show the optimal levels of K, and L that go with that optimal level of Q.
|
K |
L |
Qe |
|
10 |
||
|
20 |
||
|
30 |
||
|
40 |
||
|
50 |
||
|
60 |
||
|
70 |
Let total expenditures equal $1,100 in period 2 and $1,200 in period 3.
d) Calculate the new optimal values of Q, and the new isoquants and plot the LR Expansion Path.
e) Using data from d), keep K at 25, letting L vary, and plot the SR Expansion Path and the TPL curve.
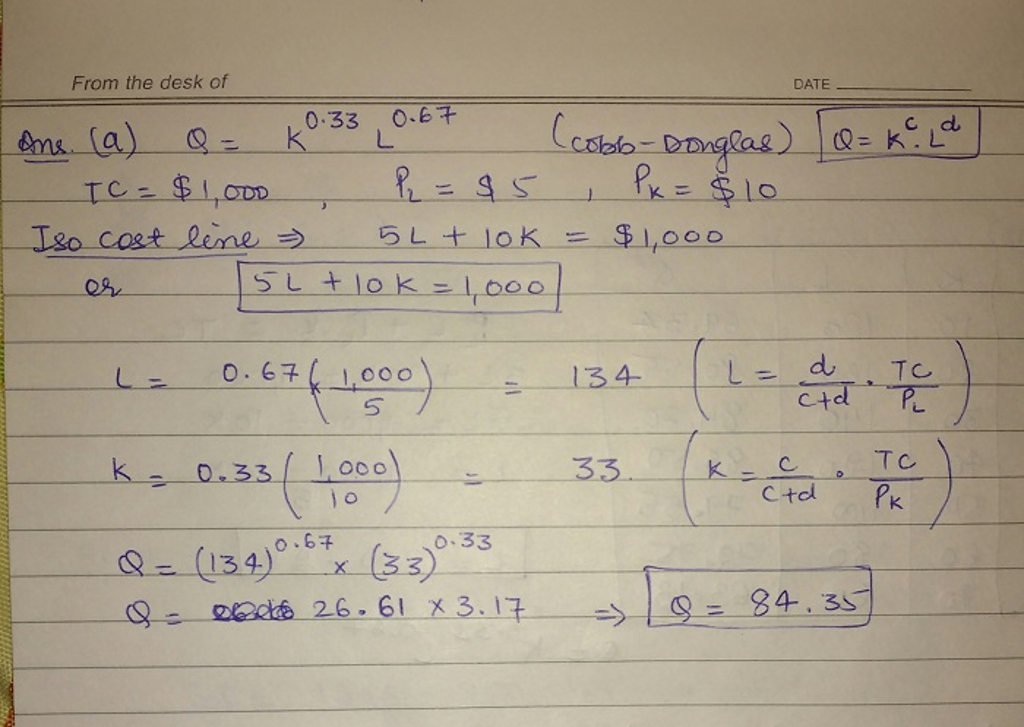


2) Let a production function exist such that Q=K.30L.75
.
a) Does this production function exhibit Increasing, Decreasing or Constant Returns to Scale? Explain what
your answer means and how you know. (Each may be answered by one or two sentences at most).
b) Estimate the effect on Q of a 10% increase in Labor hours, keeping K constant.
c) Estimate the effect on Q of a 10% increase in capital usage, keeping L constant.
- The production function Q=K.30 L0.75
It is a cobb douglas prduction function, where a=0.30 and b =0.75
a+b=1.05>1
This means this function exhibits increasing returns to scale.
b. If there is a 10% increase in labor hours, keeping K constant, then Q will increase by 7.5%. (.75*10).
c. If there is a 10% increase in capital usage, keeping L constant, then Q will increase by 3%. (.30*10).
3) The Halogen Company is a member of the lamp industry.
The price of a lamp is $200.
Fixed costs run $1,000
The firm’s total cost function is
TC=$1,000+20Q+5Q2
where TC is total cost (in dollars) and Q is hourly output.
a) Is this firm a perfectly competitive firm or not? How can you tell? Explain in detail.
b) What output maximizes profit? Graph results.
c) What is the $ value of the firm’s profit at this output level?
d) What is the firm’s average cost at this output?
e) Will/should this firm shut down? Why or why not?
a) Yes, it is a perfectly competitive ?rm.
The concept of perfect competition applies when there are many producers and consumers in the market and no single company can in?uence the pricing. Here, Halogen Company is a member of the lamp industry- so it is not a single company in the market. A perfectly competitive market has the following characteristics:
There are many buyers and sellers in the market.
Each company makes a similar product.
Buyers and sellers have access to perfect information about price.
There are no transaction costs.
There are no barriers to entry into or exit from the market.
-Being a perfectly competitive firm Halogen Company should satisfy all these conditions.
b) TR=P"‘Q=2000.
MR=dTR/dQ=2OO
TC = $1000 + 2OQ+ 50.2
MC=dTC/dQ=2O+10Q
Profit maximizing condition for perfectly competitive market is-
MC=MR
Or, 20+1OQ=2OO
Or, 1OQ=180
Or, Q=18
S0, P=$200 and Q=18
C) TC = S1000 + 20Q+ SQ2 =1000+360+1620=2980
Firm's profit=TR-TC=$(3600-2980) =S620
d) Firm's average cost=TC/Q=$(1000 + 200+ SQ2)/Q=2980/18=$165.56
e) The firm should produce its output until its price is greater than average variable cost.
TC = S1000 + 20Q+ 50.2
Here, fixed cost is S1000 and variable cost is 20Q+5Q2
Average variable cost=dVC/dQ=20+1OQ
Placing value of Q in the equation we get,
AVC=20+180=200
It is given P=$200
So, we get that, here P=AVC
After that level the firm should shut down its production. Otherwise it will loss if it goes for further production.
4) Let Market Supply for apartments be P=$200+.50QS
Let Market Demand for apartments be P=$1700-.75QD
a) Calculate the optimal quantity and rent per month on apartments.
b) Calculate the Consumer and Producer Surplus arising from the competitive output.
c) Calculate the Deadweight loss at this price and quantity.
Let the rent control board mandate a rent of only $550.
d) Calculate the new quantity of apartments supplied to the market.
e) Calculate the quantity that would be demanded at that rent.
f) Calculate the amount of CS gained if a rent control occurred (and the new price was set at $550 per month).
g) Calculate the amount of Consumer and Producer Deadweight loss arising due to the rent control.
- The equilibrium or the optimal price of demand and supply must be same so
$200 + .50QS = 1700 - .75Qd
1.25Qd =1500
Qd= 1500/1.25 =120O
P =200+0.5*1200 = 800
- Consumer Surplus
At Q=0 Pd = 1700
CS = 0.5"‘(1700—800)"‘12OO = 540,000
Producer surplus
At Q=0 Ps = 200
PS = 0.5"‘(800—200)"‘1200 = 360,000
- Deadweight Loss will be zero.
- $200 + .50QS = 550
Qs = (550 - 200 ) / 0.50
Qs = 700
- 1700 - .75Qd = 550
Qd = (1700 -550) / 0.75
Qd = 1533.33
- Gain in CS = New CS - Old CS
New CS = 1/2 x Base (Q) x Height (WTP -P)
= 1/2 x (1700 - 550) x 1533.33
= 881664.75
Gain= 881664.75- 540,000 => 341664.75
- Dead weight Loss = Area of triangle whose base is change in Q and Height is change in P
DWL = 1/2 (1200 - 700) x (800 - 550)
DWL = 1/2 x 500 x 250
Total DWL = 62500
DWL to consumers and producer is same = 1/2 x 62500 => 31250
5) Given the following table of costs, productivities and revenues,
(reproduce in your answer and fill in missing values)
|
P*Q |
w*L |
MPL*MR |
||||||||
|
L |
TP=Q |
MPL |
APL |
Price |
TR |
MR |
Wage |
TRC |
MRC |
MRP |
|
1 |
0.2 |
0.2 |
150 |
30 |
80 |
|||||
|
2 |
1 |
145 |
145 |
85 |
||||||
|
3 |
2.4 |
150 |
360 |
95 |
||||||
|
4 |
2.8 |
135 |
378 |
100 |
||||||
|
5 |
3 |
130 |
390 |
115 |
||||||
|
6 |
2.7 |
125 |
337.5 |
125 |
determine:
a) The optimal quantity of input L used.
b) The optimal wage paid
c) The general type of output market this firm finds itself in (perfectly competitive or imperfectly
competitive). Justify your answer.
d) The general type of input market this firm finds itself in (perfectly competitive or imperfectly competitive).
Justify your answer.
e) Graph appropriately, noting important results.
Expert Solution
Need this Answer?
This solution is not in the archive yet. Hire an expert to solve it for you.







