Why Choose Us?
0% AI Guarantee
Human-written only.
24/7 Support
Anytime, anywhere.
Plagiarism Free
100% Original.
Expert Tutors
Masters & PhDs.
100% Confidential
Your privacy matters.
On-Time Delivery
Never miss a deadline.
Suppose that you purchased three types of financial assets, A, B and C
Suppose that you purchased three types of financial assets, A, B and C. The returns from the assets in the past 5 days are reported in the following table: ? B 1 -4 ? 20 20 3 2 day 1 day 2 day 3 day 4 day 5 5 10 -10 20 2 4 4 8 -10 Based on the data, we calculate the covariance matrix with some blank entries: AB C ? B 6.4 24 C-18 (??) 216 (a) Complete the covariance matrix by filling in the blank entries, (?) and (??). Use the population version of variance and covariance formula. (b) If you expect the returns from C to drop next year, how would you expect the returns from A based on the covariance? How about the returns from B? (c) Compare the relationships of pair A&C and pair B&C. Determine which pair has the stronger relationship. (d) Consider portfolio X that invests 70% in B and 30% in C. Find the mean and standard deviation of returns from each portfolio. Compare the new portfolio with the original assets B and C.
Expert Solution
The variance of a population variable 'X' can be calculated by the following formula
Var (X) = 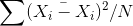
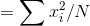
Where 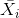 is mean value, N is the population size and
is mean value, N is the population size and 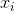 is the deviation from the mean value.
is the deviation from the mean value.
The formula for covariance between two variables is given as
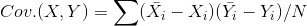
Therefore according to the question,
the mean values of returns from the assets A, B and C in 5 days can be calculated as
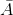 = 3 ,
= 3 , 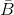 = 4 and
= 4 and 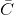 = 8
= 8
deviations from the mean is given as
| A | B | C |
| 2 | 8 | -12 |
| 0 | 2 | -12 |
| -2 | -6 | 18 |
| 1 | 0 | -12 |
| -1 | -4 | 18 |
squared of deviations from the mean value is given in the following table
| Days/Assets | A | B | C |
| 1 | 4 | 64 | 144 |
| 2 | 0 | 4 | 144 |
| 3 | 4 | 36 | 324 |
| 4 | 1 | 0 | 144 |
| 5 | 1 | 16 | 324 |
| Total | 10 | 120 | 1084 |
Var (A) = 10/5 =2
Cov. (B, C) = (-96-24-108+0-72)/5 = 300/5 = 60
Solution (a) : covariance matrix
| A | B | C | |
| A | 2 | ||
| B | 6.4 | 24 | |
| C | -18 | 60 | 216 |
Solution (b)
If the returns from C is expected to be drop in next year, then based on the covariance between A and C, it is expected that returns from A will increase in next year as they have negative sign of covariance coefficient. Also, it is anticipated that returns from asset B will drop down in next year based on the covariance between B and C.
Solution (c)
Pair A and C have covariance of -18 whereas that of between pair B and C is 60. Pair B and C have shown high strength of positive covariance that is if there is change in returns of B, returns from C will also change in the same direction and vice-versa.
Solution (d)
Standard deviation in two assets B and C portfolio
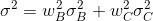
where sigma is standard deviation, 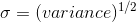
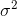 = (0.70)(24) + (0.30)(216) = 16.8 + 64.8 = 81.6
= (0.70)(24) + (0.30)(216) = 16.8 + 64.8 = 81.6
standard deviation = (81.6)^1/2 = 9.03
Archived Solution
You have full access to this solution. To save a copy with all formatting and attachments, use the button below.
For ready-to-submit work, please order a fresh solution below.







