Fill This Form To Receive Instant Help
Fill This Form To Receive Instant Help
Homework answers / question archive / 1)How much interest would the person save if he paid off his mortgage over 15 yrs instead of 30 yrs? his mortgage is 100k at 6 percent interest calculated semi annually
1)How much interest would the person save if he paid off his mortgage over 15 yrs instead of 30 yrs? his mortgage is 100k at 6 percent interest calculated semi annually. a. 62959 b 64111 c.107069 d. 58297
2)The life expectancy of a particular brand of tire is normally distributed with a mean of 40,000 and a standard deviation of 5,000 miles. What is the probability that a randomly selected tire will have a life of at least 35.000 miles? 2.0.1587 6.0.8413 0 0.0000 4.1.0000.
3)There are two different types of companies in the market: Good companies earning a rate of return of 6% for sure. Bad companies earning a rate of return of either 0% or 16% with equal chance. Furthermore, you know that there are just as many Good Companies as Bad Companies, however, you have no way to identify which type an individual company is. Please calculate to two decimals. Note that the % sign should not be included in your answer, because it is already written in the text. if a bank is charging 5% for loans, would both types of companies apply for a loan? Answer Yes/No: Is there a chance that some of the companies are unable to repay the loan plus interests? Answer Yes/No: 96. As a result the expected return for the bank would be Repeat for the case of 6% interest rate on loans. The expected return for the bank would then be 96. Repeat for the case of 7% interest rate on loans. The expected return for the bank would then be 96. Repeat for the case of 8% interest rate on loans. The expected return for the bank would then be % Repeat for the case of 9% interest rate on loans. Would any company apply?
1)=PMT((1+6%/2)^(2/12)-1,12*30,-100000)*12*30-PMT((1+6%/2)^(2/12)-1,12*15,-100000)*12*15
=62959
2)
Mean = 40,000
Standard Deviation = 5,000
Observation = 35,000
z value = (Observation - Mean) / Standard Deviation
z value = (35,000 - 40,000) / 5,000
z value = -1
Probability of a type having a life span of atleast 35,000 miles = P(z > -1)
Probability of a type having a life span of atleast 35,000 miles = 1 - P(z < -1)
Probability of a type having a life span of atleast 35,000 miles = 1 - P(-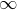
< z < -1)
Using the Normal distribution table we get P(-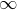 < z < -1) = 0.15866
Probability of a type having a life span of atleast 35,000 miles = 1 - 0.15866
Probability of a type having a life span of atleast 35,000 miles = 0.84134
3)Rate of Earnings :-
For Good Companies = 6%
For Bad Companies = 0% or 16% with equal chance
So overall it can be said that the bad companies earnings will be 0%x50% + 16%x50% = 8%.
If a bank is charging 5% for loans, would both types of companies apply for Loan?
Answer - Yes.
This is because Good companies are earning at 6% and will definitely apply for a loan with 5%.
Further, bad companies are earning an overall rate of 8% and hence will also apply for the loan.
Is there a chance that some of the companies are unable to repay the loan plus interest?
Answer - Yes.
bad companies which are earning at a rate of 0% will be unable to repay the loan plus interest to the bank and the chances of which are 50%.
As a result the expected return for the bank would be ____ %.
The bank is charging 5% for loans, hence the entire 5% is earning for them.
Now, the good companies and the bad companies (with 16% earnings) will repay the loan with interest and hence the bank will earn 5%.
However, bad companies (with 0% earnings) will default on the loan and might not be able to repay the loan with interest. And the bank will lose the 5%.
For the purpose of calculation lets assume four companies. Since we know that there are as many good companies as bad companies, hence
2 Good Companies
1 Bad Company with 0% earning
1 Bad Company with 16% earning
Therefore the expected return for the bank would be
5%x50% + 5%x25% + 0%x25% = 3.75 (Answer)
Repeat for the case of 6% interest on loans. The expected return for the bank would be ____ %.
The bank is now charging 6% for loans, hence the entire 6% is earning for them.
Now, the good companies earning 6% will just earn exactly that is required by the bank and the bad companies (with 16% earnings) will repay the loan with interest and hence the bank will earn 6%.
However, bad companies (with 0% earnings) will default on the loan and might not be able to repay the loan with interest. And the bank will lose 6%.
For the purpose of calculation lets assume four companies. Since we know that there are as many good companies as bad companies, hence
2 Good Companies
1 Bad Company with 0% earning
1 Bad Company with 16% earning
Therefore the expected return for the bank would be
6%x50% + 6%x25% + 0%x25% = 4.5 (Answer)
Repeat for the case of 7% interest on loans. The expected return for the bank would be ____ %.
The bank is now charging 7% for loans, hence the entire 7% is earning for them.
Now, the good companies earning 6% will just be unable to repay the loan and will default. The bad companies (with 16% earnings) will repay the loan with interest and hence the bank will earn 7%.
However, bad companies (with 0% earnings) will default on the loan and might not be able to repay the loan with interest. And the bank will lose 7%.
For the purpose of calculation lets assume four companies. Since we know that there are as many good companies as bad companies, hence
2 Good Companies
1 Bad Company with 0% earning
1 Bad Company with 16% earning
Therefore the expected return for the bank would be
0%x50% + 7%x25% + 0%x25% = 1.75 (Answer)
Repeat for the case of 8% interest on loans. The expected return for the bank would be ____ %.
The bank is now charging 8% for loans, hence the entire 8% is earning for them.
Now, the good companies earning 6% will just be unable to repay the loan and will default. The bad companies (with 16% earnings) will repay the loan with interest and hence the bank will earn 8%.
However, bad companies (with 0% earnings) will default on the loan and might not be able to repay the loan with interest. And the bank will lose 8%.
For the purpose of calculation lets assume four companies. Since we know that there are as many good companies as bad companies, hence
2 Good Companies
1 Bad Company with 0% earning
1 Bad Company with 16% earning
Therefore the expected return for the bank would be
0%x50% + 8%x25% + 0%x25% = 2.00 (Answer)
Repeat for the case of 9% interest on loans. The expected return for the bank would be ____ %.
The bank is now charging 9% for loans, hence the entire 9% is earning for them.
Now, the good companies earning 6% will just be unable to repay the loan and will default. The bad companies (with 16% earnings) will repay the loan with interest and hence the bank will earn 9%.
However, bad companies (with 0% earnings) will default on the loan and might not be able to repay the loan with interest. And the bank will lose 9%.
For the purpose of calculation lets assume four companies. Since we know that there are as many good companies as bad companies, hence
2 Good Companies
1 Bad Company with 0% earning
1 Bad Company with 16% earning
Therefore the expected return for the bank would be
0%x50% + 9%x25% + 0%x25% = 2.25 (Answer)
