Fill This Form To Receive Instant Help
Fill This Form To Receive Instant Help
Homework answers / question archive / You are given the following autocorrelations for a sample of 100 observations: Lag ACF 1 2 3 0
You are given the following autocorrelations for a sample of 100 observations: Lag ACF 1 2 3 0.032 0.104 0.420 and are reminded of the following formula Q* = T(T + 2) =12xmUsing the Ljung-Box test at the 5% significance you conclude that: Select one: A. There is some autocorrelation of up to order 3 B. There is some autocorrelation of up to order 1 C. There is some autocorrelation of up to order 2 D. None of these E. There is no autocorrelation of up to order 3 O
The test will be conducted for 3 seperate cases,
(i) m =1 (lag =1)
here, T = 100,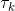 
= 0.032,
Q* = 100*(100+2)*[(0.032)^2]/(100 - 1) = 0.1055
Q ~ X^2 with 1 degree of freedom
Q(0.05,1) = 3.841
Since, Q* < 3.841, We may accept the null, i.e there is no autocorrelation of order 1
(ii) m =2
here, Tau1 = 0.032 and Tau2 = 0.104
Q* = 100*(100+2)*{[(0.032)^2]/(100 - 1) + [(0.104)^2]/(100-2) } = 1.2312
Q ~ X^2 with 2 degrees of freedom
Q(0.05,2) = 5.991
Clearly Q* < 5.991, therefore we may reject the null hypothesis, and conclude
there is no significant autocorrelation at lag of order 2.
(iii) m =3
here, Tau1 = 0.032 Tau2 = 0.104, Tau3 = 0.420
Q* = 100*(100+2)*{[(0.032)^2]/(100 - 1) + [(0.104)^2]/(100-2) + [(0.420)^2]/(100-3) } = 19.7805
Q ~ X^2 with 3 degrees of freedom
Q(0.05,3) = 7.815
here, Q* >. 7.815, thus we may reject the null hypothesis and conclude that there is a significant autocorrelation at lag of order 3.
Thus option A is correct.
